E-Archive
Science Update
in Vol. 19 - July Issue - Year 2018
Optimisation Of The Shot Peening Control Factors By Using The Taguchi Based-Fuzzy Logic Methodology

Table 1: Shot peen factors and their levels
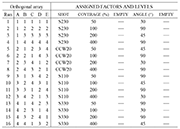
Table 2: Fractional factorial array L16(45) with factors and levels assigned to columns

Figure 1: Architecture of the fuzzy inference unit
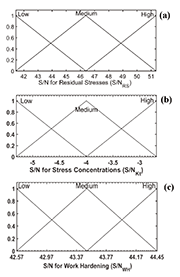
Figure 2: Selected membership function distributions for shot peening effects in terms of S/N: (a) Residual stresses, (b) stress concentrations and (c) work hardening
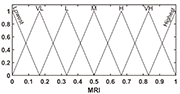
Figure 3: Membership functions for the MRI

Table 3: The fuzzy rules
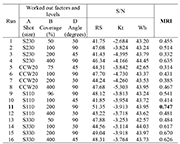
Table 4: Results of the design of experiments analysis and fuzzy reasoning for MRI
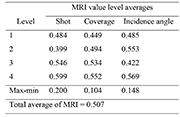
Table 5: Response table for MRI at each level of the process parameters
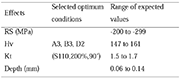
Table 6: Estimated optimum peening conditions
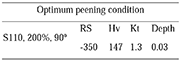
Table 7: Experimental peened effects determined from the estimated peening conditions of table 6
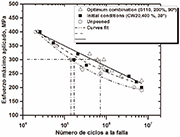
Figure 4: Axial loading, constant amplitude S-N curves for peened and unpeened 2024-T351 AA
Introduction
The shot peening process causes the surface of metallic components to be strengthened through bombardment with a torrent of minute balls named shots, thus inducing significative responses such as compressive residual stresses, surface hardening and surface roughness. In the aerospace, automotive, shipping and manufacturing industries, proper selection and control of peening factors is highly required to ensure a real benefit mainly in terms of fatigue resistance. In the present research, the Taguchi methodology coupled with the fuzzy logic is used for determining the best selection of the control factors that directly influence the multi-objective response properties of a peened 2024-T351 aluminium alloy (AA). The input parameters taken into consideration are shot, coverage and incidence angle. For statistical purposes, the experimental parameters were put in place with a L16 orthogonal fractional array. The three induced properties extracted experimentally from the treated AA are fed as inputs to the fuzzy inference system and the only output is the response index (MRI). The validation test carried out to validate the results confirmed that the approach used in this work can effectively provide the optimum parameters by virtue of obtaining an improvement in fatigue resistance.
Design of experiments through the Taguchi method
Although design of experiments can take many forms, this strategy aims to quantitatively identify both the main effects of the factors and any interaction between them. This method also allows for conclusions to be drawn that are valid over a range of experimental conditions [1]. The basic steps involved in any design of experiments analysis consist of assuming a set of variables controlling the output function, selecting the number of levels of each variable to test, and picking the proper factorial array. Even though the choice of a particular approach will depend on the number of factors and levels, the use of fractional factorial method (also known the orthogonal array) represents itself as the most reasonable choice in terms of reducing the number of experiments without loss of quality in the obtained results [2]. A total of three factors were evaluated at four levels without interaction, each as shown in Table 1. These chosen factors are of fundamental importance to the aircraft industry [3]. A complete full factorial design that would allow for estimation of all main effects and factor interactions would require 43 or 64 experiments. However, taking into account that an orthogonal experimental design depends upon degree of freedom (DOF), the number of experiments was determined to be 18. Assuming that higher order interactions between factors were negligible, one-fourth fractional factorial design evolving a total of 16 experiments was selected.
A fractional factorial L16(45) array was the choice to enable the optimisation of five parameters with each of these set at a maximum of four levels. This approach permitted the estimation of all main and first-order factor interactions. Furthermore, as this array is built to be used for five factors, there was a need to leave a couple of columns empty. This latter aspect positively supports the experimental design because all important parameters influencing shot peening effects are considered. The full fractional factorial array together with the selected factors and levels is depicted in Table 2.
In this piece of research, "the smaller the better" was assigned as the surface roughness factor. Its estimation is given as:
"formula cannot be displayed online" (1)
where Yi is the experimental value of the ith trial, and n is the number of trials. For the residual stresses and work hardening properties, the larger the better estimation can be defined as:
"formula cannot be displayed online" (2)
Taguchi-fuzzy logic methodology
Fuzzy logic uses conventional language to define variables and utilises fuzzy linguistic rules to describe relationships instead of working with numeric values of variables and using mathematical functions.
The structure of a fuzzy inference system (FIS) is constituted by a fuzzifier, membership functions (MF), a fuzzy rule base, an inference engine, and a defuzzifier [4]. This is shown schematically in Fig. 1. In the FIS, the input and output variables are coded in a fuzzy representation, whereas the relationships are governed by "if then" rules.
The fuzzifier is utilised to transform the input data (crisp values), into suitable linguistic variables, which may be envisaged as linguistic terms for fuzzy subsets. Three fuzzy subsets (Low, Medium and High) are uniformly assigned to the three input variables, namely, the S/N ratios for residual stresses (S/NRS), surface roughness in terms of stress concentrations (S/NKT) and work hardening (S/NWH). The values of the input data must be defined as MF. An MF can take different forms such as bell, Gaussian, sigmoidal, triangular, and trapezoidal shape, or a combination of shapes for each input. In the present work, triangular MF’s were used for the input S/N ratios owing to high computational efficiency and simplicity to fuzzify the inputs and outputs (Fig. 2).
Seven fuzzy subsets (Lowest, Very Low, Low, Medium, High, Very High and Highest) are assigned to the single output MRI (Fig. 3).
The modified S/N ratios are sent to the inference engine where the corresponding fuzzy rules are applied. In this endeavour, the Mamdani method was adopted as the inference engine, which is based on the collection of if-then rules. The fuzzy rule base accrued three inputs, S/NRS, S/NKT and S/NWH, and one output MRI. These are given as:
• Rule 1: if S/NRS is Low and S/NKT is Low and S/NWH is Low then MRI is Lowest
• Rule 2: if S/NRS is Low and S/NKT is Low and S/NWH is Medium then MRI is Very Low
...
• Rule 27: if S/NRS is High and S/NKT is High and S/NWH is High then MRI is Highest
Various degrees of membership to the fuzzy sets are calculated taking into account the values of S/NRS, S/NKT and S/NWH, and MRI. Twenty-seven fuzzy rules (Table 3) were built directly based on the fact that the larger the S/N ratio, the better the performance of the characteristic.
The Mamdani system generates the output data in the form of linguistic values, which undergoes a defuzzification process. In this last stage, the defuzzifier translates the fuzzy output into a numerical form. The design of the fuzzy system was carried out using MATLAB software, through the fuzzy toolbox for Mamdani system. The results were subsequently compared with the experimental data of the peening process, to obtain the optimum values.
Taguchi fuzzy logic analysis
The evaluated effects were the calculated stress concentration factor, the measured-calculated maximum compressive residual stress, and the direct measurement of maximum microhardness. The performance statistics utilised were selected according to two modalities: (i) Larger-the-better statistic both for the maximum compressive residual stress and for the work hardening effects, and (ii) smaller-the-better statistic for the stress concentration. The experimental results previously described were further transformed into the S/N ratios of three output responses (using Eqs. (1) and (2)) based on the control factor combinations depicted in Table 4. Columns labelled "A, B and D" are a repeat of the chosen orthogonal array. These show the combinations of factor levels used for each run. Columns "S/N" show an average of the results for each of the functional behaviours. In the case of both residual stresses and work hardening, the best S/N ratio is that given by the highest value, whereas the best S/N for stress concentration (surface roughness) is the lowest value. The reason for using S/Ns is due to the fact that the engineering units of those three responses are different, hence the S/Ns estimations for each effect have to be obtained in order to unify the unit and be certain on the quality of response. The MRI for the multi-response results determined by FIS, and their order as obtained for all 16 experiments, are listed in the last column of Table 4.
The higher the value of the MRI for an experiment, the higher the chance of that experiment being the optimum. In this regard, experiment 11 has the best multiple performance characteristics among the 16 tests because it has the highest multi-response index.
The orthogonality in the experimental data makes it possible to extract the effect of each of the shot-peening parameters at different levels, when the mean is calculated for a control factor level, all of the other factors take on each of their levels an equivalent number of times. The average of the MRI for each level of the test parameters is presented in Table 5. The total mean of the MRI was also determined. This response table contains values obtained when the lowest number is withdrawn from the highest in each column. A large difference is an indicative of the significance in the contribution of the particular parameter under analysis. It can be readily deduced from the response table that the shot parameter has the highest contribution, followed by the incidence angle, and then coverage.
The resultant conditions of experiment 11 from the designed experiment is shown in Table 6.
Experimentally determined peening effects using estimated optimal combinations are shown in Table 7. The experimental data were found to be slightly different from those of Table 6. Such discrepancies can be attributed to several process factors such as: (i) variation in the pressure, (ii) wear (of the media, nozzle, and hose), (iii) highly scattered shot size, and (iv) variation in the flow rate due to interferences caused by dust, debris or other objects, among others.
Fatigue results
Conventional uniaxial tension-tension fatigue tests were carried out using hourglass specimens. Shot peening of the specimens was undertaken according to the conditions determined in the previous section. The results of fatigue tests conducted for the aluminium alloy are graphically presented in the form of Wöhler stress versus cycles to failure (S-N) curves over a wide range of applied stresses as shown in Fig. 4. The fatigue endurance is defined as the endurance stress at or below which a specimen can sustain cycling for up to 7x106 cycles without failing.
Trends observed in the fatigue life curves revealed that shot-peened specimens have a marginally superior life compared to those unpeened, specifically at an intermediate zone of the low- and high-cycle fatigue regions. It was evident however, that peening did not impair the fatigue performance of the material. Optimum peening conditions, on the whole, were found to be better as expected from the Taguchi-fuzzy logic estimations. Furthermore, there was a discernible improvement in endurance by peened specimens when tested at stresses around 300 MPa (line-dot-line in Fig. 4). The fatigue endurance for the unpeened material was approximately 190 MPa, whilst that for the peened at optimum condition was 225 MPa. No discernible difference in fatigue life was observed in the low-cyclic fatigue region (102 < cycles to failure < 105.
Final remarks
Based upon the experimental and numerical results, the following conclusions can be drawn:
The plethora of variables capable of altering the peening process, and hence fatigue life, is the reason that strict process control of all variables is necessary. The aluminium alloy 2024-T351 peened to predicted optimum conditions (S110, 200%, 90º) exhibited superior fatigue performance than peened to predicted initial conditions, and also to the unpeened surfaces. The best fatigue performance was achieved using the finest shot (S110). Surface integrity degradation precedes fatigue damage. The geometry of the indentation is a prime damage feature. The result of the confirmation experiment and fatigue testing implies that the Taguchi-fuzzy logic methodology is very effective for optimising the multi-response characteristics in shot peening within the ranges of the control factors studied.
The advantages of the Taguchi-fuzzy logic approach compared to classical methods lay in speed, simplicity, and low cost. Therefore, this approach can be considered for applications in engineering situations, as shot peening, laser peening, burnishing, water peening, etc.
References
1. George, P. M., Pillai, Nisha, & Shah, Nisha. (2004). Optimization of shot peening parameters using Taguchi technique. Journal of Materials Processing Technology, 153-154, 925-930.
2. Van Nostrand, Richard Craig. (2002). Design of Experiments Using the Taguchi Approach: 16 Steps to Product and Process Improvement. Technometrics, 44, 289-289.
3. Nam, Yong-Seog, Jeon, Ung, Yoon, Hee-Kweon, Shin, Byung-Cheol, & Byun, Jai-Hyun. (2016). Use of response surface methodology for shot peening process optimization of an aircraft structural part. The International Journal of Advanced Manufacturing Technology, 87, 2967-2981.
4. Chandrasekaran, M., Muralidhar, M., Krishna, C. Murali, & Dixit, U. S. (2010). Application of soft computing techniques in machining performance prediction and optimization: a literature review. The International Journal of Advanced Manufacturing Technology, 46, 445-464.
Affiliation:
Public Education Secretary of Mexico
Instituto Tecnológico de Tlalnepantla del TecNM
Postgraduate Office/Department of Mechanical Engineering
E-mail: jsolis@ittla.edu.mx



























