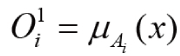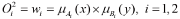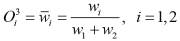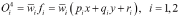1. Introduction
Shot Peening (SP) is a cold-working process that hardens the surface of a metallic component by bombarding it with a stream of small balls called shots. Generally speaking, SP is viewed as a process involving multiple and progressively repeated impacts. The indentation at each point of impact is the result of local plastic deformation. In this sense, the main parameters that control the performance of this process can be identified as media (shot), intensity, incidence angle and coverage. Due to its specific nature of the input/output data, there is a need of using one of those numerical techniques that consider non-linear statistical analysis for dealing with ill-defined and uncertain data. Logical, mathematical and statistical approaches provide elimination of inconvenient alternatives and select the most effective parameters letting make multi-criteria decisions. From an extensive list of methods, TOPIS (Technique for Order Performance by Similarity to Ideal Solution), COPRAS (Complex Proportional Assessment), GRA (Grey Relational Analysis) and SAW (Simple Additive Weighting) are widely applied on the engineering field. In this paper, GRA along with ANFIS are combined to manage from process parameters to multi-responses. On one side, GRA effectively performs the conversion of multi-response optimisation to the single objective. On the other side, a fuzzy inference system (FIS) utilising fuzzy if-then rules can model the quantitative features of human knowledge and reasoning processes without using conventional mathematical tools [1, 2]. However, FIS has a clear disadvantage in that it lacks successful learning mechanisms. The excellent property of ANFIS is that it compensates for the disadvantage of FIS with the learning mechanism of neural networks. The ANFIS architecture can be obtained by embedding the FIS into the framework of adaptive networks. In this way, the non-linear and complex relationship of the SP process parameters can conveniently be investigated on the mechanical responses through the use of the hybrid GRA-ANFIS approach. The present study proposes a hybrid approach based on GRA-ANFIS to optimise the performance characteristics of a 7150-T651 Aluminium Alloy by SP.
2. Methodology
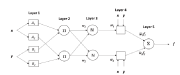
ANFIS is an artificial intelligence way used for solving complicated and nonlinear systems [3-5]. It is a data-driven procedure that can be used to provide the solution of function approximation problems in a neural network platform. Here at first, a FIS comprising of an initial fuzzy model is formed, based on the fuzzy rules extracted from the input- output data set. In the next step the neural network is used to fine tune the rules of the initial fuzzy model that was built. Using ANFIS methodology the network is trained. The structure of the ANFIS model used in this study [6] comprises node segments and five different layers (fuzzy layer, product layer, normalised layer, layer of defuzzification and output layer). Each of the layers contains several nodes described by node functions. The mechanism of fuzzy reasoning for deriving an output f given an input vector [x, y] is shown in Fig. 1. The rule base contains the fuzzy if-then rules of Takagi and Sugeno’s type [20] described as follows: If x is A and y is B then z is f (x, y), where A and B are the fuzzy sets in the antecedents and z = f (x, y) is a crisp function in the consequent. Usually f (x, y) is a polynomial for the input variables x and y. If f (x, y) is taken to be a first-order polynomial, a first-order Sugeno fuzzy model is formed. For a first-order two-rule Sugeno fuzzy inference system, the two rules may be stated as: Rule 1: If x is A1 and y is B1 then f1 = p1x + q1y + r1; Rule 2: If x is A2 and y is B2 then f2 = p2x + q2y + r2
The individual layers of the above ANFIS structure are described below:
Layer 1: Every node i in this layer is adaptive with a node function (a). where, x is the input to node i, Ai is the linguistic variable associated with this node function (Low, Medium and High for this study) and µAi is the membership function of Ai.
Layer 2: Each node in this layer is a fixed node which calculates the firing strength wi of a rule. The output of each node is the product of all incoming signals to it and is given by, (b)
Layer 3: Every node in this layer is a fixed node. Each ith node calculates the ratio of the ith rule’s firing strength to the sum of firing strengths of all the rules. The output from the ith node is the normalised firing strength given by, (c)
Layer 4: Every node in this layer is an adaptive node with a node function given by (d) where is the output of the layer 3 and is the consequent parameter set.
Layer 5: This layer comprises of only one fixed node that calculates the overall output as the summation of all incoming signals.
In Science Update Vol. 21, May issue, 2020, materials and process parameters were reported. From these data, the normalized data in terms of the grey relational are recalled in Table 1.
In this study, the Matlab ANFIS toolbox was used. The structure of proposed ANFIS networks consisted of three input variables including the GRC of the residual stresses (RS), work hardening (WH) and stress concentrations (SC). The value for output layer was the Grey Relational Fuzzy Grade (GRFG). The input space is decomposed by three fuzzy linguist variables. In this paper, triangular membership functions (MFs) were utilised to construct the suggested models. It was stablished to use twenty-seven fuzzy rules to determine the GRFG. The fuzzy rule viewer for the FIS environment (where the Mamdani inference system prevails) is shown in Fig. 2. As an example, some of the designed rules in the FIS environment are described as follows:
Rule 1: If (RS is Low) and (WH is Low) and (SC is Low) Then (GRFG is Very, Very Low).
Rule 2: If (RS is Low) and (WH is Low) and (SC is Medium) Then (GRFG is Very Low).
Rule 27: If (RS is High) and (WH is High) and (SC is High) Then (GRFG is Very, Very High).
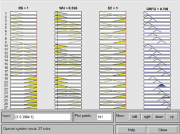
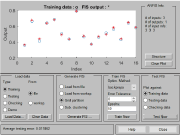
The ANFIS-GUI is created on the ANFIS editor and predicts the output. The loaded data and training data are shown in the testing data and predicted data of the interphase of Fig. 3. These training and checking data sets are collected based on the observation of the target system and are stored in separate files. The ANFIS models were trained, from 78 number of nodes. The number of linear parameters was 108, while the number of nonlinear parameters was 27, with the total number of parameters being 135. The number of training data pairs was 16. The number of checking data pairs: 0; the number of fuzzy rules: 27. Furthermore, up to 50 epochs were specified for the training process to assure the gaining of the minimum error tolerance. Backpropagation optimisation method for training the FIS was selected in this study due to the fact that is widely used for engineering applications. In order for obtaining the ANFIS grades, the GRC’s must be introduced in the fuzzy rule viewer of ANFIS. The fuzzy rule viewer for the ANFIS environment (once the Mamdani inference system is converted into the Sugeno inference system through a few particular commands of Matlab) is shown in Fig. 4.
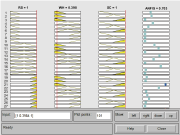
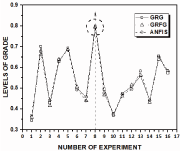
The grey relational grade, grey relational fuzzy grade and ANFIS grade are shown in Fig. 5. The higher these (GRG, GFRG and ANFIS) grades the better the correspondence to multiple responses. The highest grade in Fig. 5 can be considered to be close to optimal; however, as can be appreciated in Fig. 5 (circled in dash), all the grades from the different approaches are very close to each other in experiment 8, with the maximum grade value. It seems to be that ANFIS is in-between the GRG and GRFG; thus, ANFIS would be the technique to be chosen for SP optimisation of the process parameters. Experiments 2 and 5 also provide high grade values for all approaches.
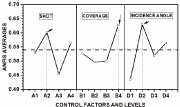
The average of the ANFIS grades for each level of the test parameters is compiled in Table 2 and plotted in the graph of Fig.6. It can be observed from the graph and the response table that the incidence angle has slightly the highest contribution compared to those of coverage and shot. Optimum conditions for the tested parameters remain alike the parameters shown in the Science Update May 2020 column. Such conditions are indicated by arrows in Fig. 6. These optimum parameters are also in line with the resulting parameters from experiment 8 as shown in Fig. 5 along with Table 1 (shadowed cell). As previously stated, the largest value for the ANFIS, i.e., run 8, corresponds to the optimum condition which satisfies the selected criteria of the multi-responses.
References
1. Zadeh, L.A., Fuzzy sets. Information and Control, 1965. 8(3): p. 338-353.
2. Sugeno, M. and G.T. Kang, Structure identification of fuzzy model. Fuzzy Sets and Systems, 1988. 28(1): p. 15-33.
3. Jang, J.-S.R., ANFIS: adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man, and Cybernetics, 1993. 23(3): p. 665-685.
4. Jang, J.-S.R., C.-T. Sun, and E. Mizutani, Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence. 1997, USA: Prentice-Hall Inc.
5. Jang, J.R. and S. Chuen-Tsai, Neuro-fuzzy modeling and control. Proceedings of the IEEE, 1995. 83(3): p. 378-406.
6. Sugeno, T.T.a.M. Derivation of fuzzy control rules from human operator’s control action. in Proc. IFAC Symp. Fuzzy Inform., Knowledge Representation and Decision Analysis. 1983.
The Author: PhD José Solis Romero
E-mail: jose.sr1@tlalnepantla.tecnm.mx
MSc. Miguel A. Paredes Rueda
MSc. Rodolfo Velázquez Mancilla
PhD Víctor A. Castellanos Escamilla
Affiliation:
Public Education Secretary of Mexico
Tecnológico Nacional de México/IT de Tlalnepantla
Postgraduate Office