E-Archive
Science Update
in Vol. 11 - January Issue - Year 2010
The Connection Between Shot Peening And Short Cracks
![Figure 1: Schematic illustration of the fatigue resistance threshold for multigrain materials expressed in terms of difficulty of initial stage I crack becoming stage II crack (after Miller [1])](https://mfn.li/storage/e-archives/article-pictures/821/2200.gif)
Figure 1: Schematic illustration of the fatigue resistance threshold for multigrain materials expressed in terms of difficulty of initial stage I crack becoming stage II crack (after Miller [1])
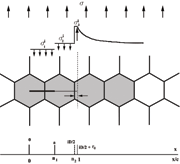
Figure 2: Schematic description of three zones representing the crack system. D is the grain diameter, r0 is the grain boundary width. The parameter i=2a/D is the normalised crack length by half grain intervals (i=1, 3, 5
Given the important concepts regarding fatigue, crack propagation regimes, some major aspects of long cracks and in more detail short crack features, it is necessary to discuss the meaning of fatigue resistance of metallic materials and its connection with both short cracks and shot peening.
The effect of the microstructural barriers decreases as crack length increases and the stress concentration at the tip of the crack gets closer and ultimately exceeds that value required to overcome the barriers. If the crack is obstructed in its path by many closely packed barriers, as would occur in microstructures containing small grains, then the crack growth path would be deflected. It is envisaged therefore that fatigue resistance is high. Herein, fatigue resistance may be quantified as the resistance to crack propagation offered by the material. Miller [1] has defined fatigue resistance for multigrain materials as the difficulty of a stage I crack becoming a stage II crack, as illustrated in Fig. 1.
To condition the surface to resist crack propagation in structural components made of aluminium alloys, the shot peening process is routinely employed for improving fatigue performance. Because this process modifies only the surface and properties of the peened surface, characterisation of fatigue damage needs to be described in terms of short crack behaviour. The shot peening process and its interaction with fatigue will be considered in detail within the following sections.
Short Cracks
The large number of papers dealing with the quantification of short crack (SC) propagation rate behaviour reported in the literature, indicate the importance of this type of fatigue crack in metallic materials. In this sense, modelling of SC propagation rate certainly has contributed to a better understanding of Microstructurally SC and Physically SC and subsequently to better fatigue-based designs. Furthermore, attributed to developments on SCs microstructural analysis, it is now possible to incorporate materials effects in an explicit form within the crack system of, e.g., a surface treated by shot peening.
The behaviour of SCs has been formulated as an answer to the belief that LEFM principles are violated due to the relatively large cyclic plasticity at the crack tip, which modifies substantially the strength of the stress field ahead of the crack. For example, a strain intensity factor that took into account cracks propagating in cyclic plastic strain fields was proposed by Boettner et al. [2], which is believed to be the first attempt to model SC propagation. A model dealing with the blocking action of grain boundaries was analysed by Chang [3], in which critical strain energy must be exceeded at the tip of a crack in order for the crack to propagate. As a result, it is argued that an incubation period arises when cracks encounter grain boundaries. A modified LEFM equation with disorientation between grains analysis was put forward by Chan et al [4]. Tanaka [5], on the other hand, considered the effect of grain boundaries on the development of slip bands and formulated the relationship of SC propagation behaviour as a function of crack tip displacement and closure. In the same work, SCs are related to the LEFM threshold stress intensity for long cracks. Hobson, Brown and de los Rios [6, 7], proposed empirical models to quantify both short and long crack propagation rates, which incorporated the effect of the microstructure in Aluminium 7075-T6 and steel. These empirical relationships were later extended by Angelova and Akid [8] in an attempt to describe more precisely short fatigue crack behaviour not only in air but in an aggressive environment.
All the above formulations, either analytically or empirically, have been reasonably successful and have served as the premise for more detailed developments which account for the elastic-plastic interface coincident with a grain boundary at any position, the successive blocking of the plastic zone by slip barriers and the subsequent initiation of slip in the next grain. A more realistic and comprehensive development is detailed in the extensive work of Navarro-de los Rios [9] who successfully related short crack propagation rate to the strength of microstructural barriers in a general model to predict the crack growth rate during stages I and II, and for both short and long cracks (applications of this formulation are given elsewhere [10]). This model predicts the decreasing crack propagation rate, and alternating fluctuations or intermittent pattern of crack growth within the microstructurally sensitive zone.
The Three Zone Micromechanical Model
Based on the analysis of distribution of dislocations by Bilby, Cottrell and Swinden (BCS) [11], Navarro and de los Rios originally proposed a theoretical model for short crack propagation by considering infinitesimal dislocations distributed within two zones, one for the crack itself and the another for the plastic zone [12]. Both bounded and unbounded solutions for the dislocation distribution system were written in a single expression, which was later further extended to incorporate a third zone to represent the situation where the blockage of the plastic zone by grain boundaries takes place. The general solution given the dislocation distribution was as follows:
“formula cannot be displayed online” (1)
where ? is the applied stress; ?i1, ?i2 and ?i3 are the friction stresses; A=Gb/2? for screw dislocations, or A=Gb/2?(1-?) for edge dislocations, G is the shear modulus, b the Burgers vector, and ? the Poisson ratio. Grain boundaries are situated at x = ½ iD and crack tips at ai = nc with c = ½ iD + r0. Here D is the grain diameter and r0 may be considered as the width of the grain boundary itself. The variable ? = x/c relates the position throughout, in such a way that the crack tip is at ? = ni1 and the nearest grain boundary at ? = ni2. Finally, the value of i = 1, 3, 5, …. describes the number of half grains affected by the fatigue process.
The friction stress ?3 represents the stress at the grain boundary and is calculated by making the bracketed term multiplying the singularity in Eq. (1) equal to zero, resulting in the following relationship:
“formula cannot be displayed online” (2)
As the crack propagates ?3 increases in value and will reach a level equal to the strength of the boundary when the crack reaches a critical length denoted by ni1 = nic. The grain boundary will be overcome and crack tip plasticity is able to extend to the next grain boundary where it is again blocked. However, if ?3 does not attain the level of the grain boundary strength before the crack tip reaches the barrier, the crack arrests.
The crack system (the term considers the crack, the crack tip plasticity and the barrier zone) can be represented by three zones as shown in Fig. 2. The first zone represents the crack itself, the second the crack plasticity and the third the barrier. In terms of stresses, the crack is envisaged as stress free unless some closure stress, ?i1, is acting on the crack flanks, the plastic zone is subjected to the stress ?i2 which represents the resistance of the material to plastic deformations (cyclic or monotonic yield stress), and the grain boundary is subjected to a stress, ?i3. This stress represents a measurement of the reaction stress developed at barrier due to the PSB blocking.
On the other hand, crack propagation rate is assumed to be proportional to the displacement between the crack surfaces at the crack tip, i.e., crack propagation rate as a function of the CTOD, also denoted as ø, as annotated in Eq. (3) [13], which through a Paris type relationship is given by:
“formula cannot be displayed online” (3)
where coefficient C and exponent m are obtained by correlating ø with long crack propagation data generated using fracture mechanics specimens.
The equilibrium equation (2) incorporates all the forces, internal and external, e.g. applied stress minus resistances and the forces due to the dislocations. A general solution was given in [14]. The application of this solution to the three-zone crack system renders expressions for crack tip open displacement (CTOD) and the constraint stress ?3. CTOD is equal to the number of dislocations entering the plastic zone, multiplied by the Burgers vector. It has been mathematically expressed as:
“formula cannot be displayed online” (4)
where b is the Burgers vector, A=Gb/2? for screw dislocations and A=Gb/2? (1-?) for edge dislocations; G is the shear modulus and ? is the Poisson ratio.
Life predictions are obtained by integrating Eq. (3) in each grain and then adding together to compute total life. The integration is made between the limits of initial crack length in each grain interval (ais) and final length in each grain interval (aif), as follows:
“formula cannot be displayed online” (5)
This total life is given by
“formula cannot be displayed online” (6)
Summarising, the important features of the model described above, are:
i. The model involves plastic displacements throughout the crack system in such a way that the tip plasticity effects are incorporated.
ii. With the introduction of the third zone which represents the blockage source or the grain boundary itself, the stress remains finite anywhere in the crack system. The grain orientation factor mi, which considers the increasing number of grains being traversed by the crack front, has been taken into account (mi increases from 1 to 3.07). Work hardening has also been incorporated, which produces more realistic predictions.
iii. Even though the model was originally developed for the prediction of short crack propagation, propagation of longer cracks has also been predicted.
iv. As the model is based on EPFM concepts it takes into account cases of large scale yielding.
v. The friction stresses in the crack wake are not modeled as a continuum closure pressure but as being a resistance to crack opening.
vi. The model describes the fatigue damage from crack initiation to catastrophic failure.
Concluding Remarks
As shot peening alters the microstructure and properties of the peened layer, characterisation of fatigue damage in peened surfaces needs to be done in terms of short crack behaviour. The microstructural fracture mechanics methodology described in this paper makes it now possible to incorporate the mechanical driving force of crack propagation, represented by the applied stress and crack length, and the material crack resistance. There is a clear possibility of including the compressive residual stress and the work hardening effects due to peening into the CTOD assessment, so as to obtain realistic estimations of fatigue life.
References
[1] Miller, K. J. “Materials science perpective of metals fatigue resistance”. Materials Science and Technology. Vol. 9, pp. 453-462. (1993).
[2] Boettner, R.C., Laird, C. and McEvily, A.J. “Crack nucleation and growth in high strain-low cycle fatigue”. Transactions of Metallurgical Society, AIME. Vol. 233, pp. 379-385. (1965).
[3] Chang, R., Morris, W.L. and Buck, O., “Fatigue crack nucleation at intermetallic particles in alloys-A dislocation pile-up model”. Scripta Metallurgica. Vol. 13, p. 191. (1979).
[4] Chan, K.S. and Lankford, J., “A crack tip model for the growth of small fatigue cracks”. Scripta Metallurgica. Vol. 17, pp. 529-538. (1983).
[5] Tanaka, K., “Modelling of propagation and non-propagation of small cracks”. In: In Small Fatigue Cracks. Ed. Ed. Ritchie R.O. and Lankford J. Metallurgycal Society Inc.: pp. 343-362. (1986).
[6] Hobson, P. D., “The formulation of a crack growth equation for short cracks”. Fatigue and Fracture of Engineering Materials and Structures. Vol. 5, No. 4: pp. 323-327. (1982).
[7] Hobson, P.D., Brown, M.W. and de.los.Rios, E.R, “Two phases of short crack growth in a medium carbon steel”. In: The behaviour of short fatigue cracks, EGF Pub. Sheffield, U.K. Eds. K.J. Miller and E.R. delosRios. Mechanical Engineering Publications, London: pp. 441-459. (1986).
[8] Angelova, D. and Akid, R., “A note on modelling short fatigue crack behaviour”. Fatigue and Fracture of Engineering Materials and Structures. Vol. 21, pp. 771-779. (1998).
[9] Navarro, A. and de.los.Rios, E.R., “A model for short fatigue crack propagation with an interpretation of the short-long crack transition”. Fatigue and Fracture of Engineering Materials and Structures. Vol. 10, No. 2: pp. 169-186. (1987).
[10] Xiaojiang, Xin, Experimental and theoretical aspects of microstructural sentive crack growth in Al-Li 8090 alloy. PhD thesis, Department of Mechanical Engineering, Sheffield: The University of Sheffield. (1992).
[11] Bilby, B.A., Cottrell, A. H. and Swinden, K. H., “The spread of plastic yield from a notch”. Proc. R. Soc. Lond. A. Vol. A-272, pp. 304-314. (1962).
[12] Navarro, A. and de.los.Rios, E. R., “Compact solution for a multizone BCS crack model with bounded or unbounded end conditions”. Philosophical Magazine A. Vol. 57, No. 1: pp. 43-50. (1988).
[13] De.los.Rios, E.R., Mohamed, H.J. and Miller, K. J., “A micro-mechanics analysis for short fatigue crack growth”. Fatigue and Fracture of Engineering Materials and Structures. Vol. 8, No. 1: pp. 49-63. (1985).
[14] Navarro, A. and de.los.Rios, E.R., “Fatigue crack growth modelling by successive blocking of dislocations”. Proc. R. Soc. Lond. A. No. 437: pp. 375-390. (1992).
The Authors:
J. Solis-Romero (PhD)
E-mail: josesolis@infinitum.com.mx
M. Paredes (MsC)
O. A. Gómez (MsC)
B. Vargas-Arista (PhD)
A. Anguiano (PhD)
Affiliation:
SEP-DGEST-IT de Tlalnepantla




























